LA CURVA DI DISTRIBUZIONE NORMALE E LE OPZIONI
Ben ritrovati.
Nella prima parte di questo lavoro siamo partiti dal problema di prezzare le opzioni, partendo dal presupposto che si trattava di un asset derivato, ossia un asset il cui prezzo deriva da quello di un sottostante (il valore della tua put IBM dipende – tra l’altro – dal valore dell’azione IBM).
Alla fine, ci eravamo soffermati su di un punto che riprendiamo dalla parte 1:
Il premio (prezzo) di un’opzione dipende dalla probabilità che il prezzo (valore) del sottostante, quando l’opzione scade, sia ad un livello tale da mettere l’opzione In The Money (ITM), cioè sia più alto dello strike price (prezzo di esercizio) della call o più basso dello di quello della put.
Mettiamo per un attimo da parte le distribuzioni e la statistica e mettiamoci nei panni di chi deve fare un prezzo, ossia deve valutare quanto è disposto a pagare per acquistare il diritto che gli deriva dall’opzione, oppure quanto vuole per assumersi il rischio legato all’opzione.
Avrai capito che stiamo parlando del potenziale compratore o del potenziale venditore dell’opzione, ma piuttosto che immergerci in matematiche complesse, proviamo a fare un salto indietro nel tempo.
Se hai seguito la prima lezione del corso gratuito “Options Fundamentals”, ricorderai che addirittura Talete di Mileto, 600 anni prima di Cristo, si dilettava con qualcosa di simile alle opzioni, i frantoi e le olive (greche, naturalmente) e, certamente, sia Talete, sia i proprietari dei frantoi si saranno confrontati col problema di dover fare un prezzo
Come lo risolsero qualche millennio prima di Black & Scholes e della loro formula?
Ovviamente non lo sappiamo. Tuttavia, facendo un salto in tempi più vicini a noi, possiamo trovare qualche interessante indizio.
Allora, immaginiamo di tornare indietro nella nebbiosa Londra vittoriana, dove Mr. Leonard Higgins, un trader dei tempi, ci farà scoprire qualcosa di interessante.
LONDRA, 1896
Alla fine del secolo XIX, “London is the par excellence option market of the world”. Ce lo racconta Leonard Higgins che, proprio nel 1896, scrive un libro, intitolato “The Put and the Call”, nel quale ci spiega il modo in cui lui (e verosimilmente i suoi colleghi) prezzavano le opzioni nella Belle Époque.
Tranquillo, non abbiamo intenzione di annoiarti con tutti i dettagli dei calcoli proposti da Mr. Higgins, ma vogliamo evidenziare un aspetto chiave, che costituisce un trait d’union non solo tra il nostro amico Leonard, in tuba e marsina, e i quant trader dei nostri giorni, ma anche (e soprattutto) i nostri discorsi e la curva di distribuzione normale che abbiamo conosciuto nella prima parte.
Sia moderni option trader, sia i loro predecessori nel XIX secolo facevano riferimento alla fluttuazione dei rendimenti azionari per stimare i prezzi delle opzioni. La differenza fondamentale sta nel fatto che oggi si fa riferimento ai concetti di varianza e deviazione standard (la standard deviation di cui abbiamo parlato nella puntata precedente); nel passato, ai tempi del libro, si usava la media degli scostamenti assoluti (in sostanza, la media degli scostamenti dalla media).
Ora, al di là dello strumento statistico utilizzato, il punto chiave è che, ora come allora, NON è il il rendimento atteso dell’attività sottostante il fattore che ha un effetto diretto sul prezzo dell’opzione, ma la variabilità dei rendimenti, tanto che le opzioni diventano principalmente strumenti per operare sulla volatilità.
NON DOVE, MA QUANTO SI MUOVE…
Già nella precedente puntata, nel caso delle opzioni, avevamo sottolineato l’importanza di quanto si muova il sottostante. Oggi, aggiungiamo la considerazione che il “quanto” si muove è in effetti la vera variabile, piuttosto che la direzione del movimento stesso, ai fini della determinazione del prezzo di un’opzione.
Ricorderai anche che, parlando di distribuzioni, ossia del modo di manifestarsi della variabilità di certi fenomeni, notammo che
- Un valore baricentrico, come la media, insieme alla SD ci permettono di attribuire un certo grado di probabilità al verificarsi di una data occorrenza del fenomeno stesso;
- Qual è la condizione? Semplice: le manifestazioni di quei fenomeni devo essere distribuite “normalmente”, ossia secondo le regole e i parametri della curva di distribuzione normale anche detta Gaussiana. Ricordi il college? Se abbiamo l’altezza media dello studente e la SD, sapendo che le altezze sono normalmente distribuite, possiamo ipotizzare in quali intervalli si addenserà l’altezza del maggior numero di studenti.
Il passo successivo consisterà nell’applicare i concetti che abbiamo visto sin qui ai prezzi di un asset finanziario, un’azione, un indice, etc.
Il presupposto di partenza è la c.d. Random-walk hypothesis, che, in buona sostanza, dice che l’andamento e l’evoluzione del prezzo di mercato di un asset NON può essere previsto, ma segue un andamento casuale.
Se volessimo semplificare all’estremo, il modello raffronta i cambiamenti di prezzo di un titolo al lancio della più classica delle monetine e, proprio come gli esiti di numerosi lanci della moneta tendono a distribuirsi “normalmente”, così, secondo il modello, i futuri rendimenti di un titolo tenderanno ad assumere la configurazione d’una distribuzione normale, proprio come quella raffigurata di seguito.
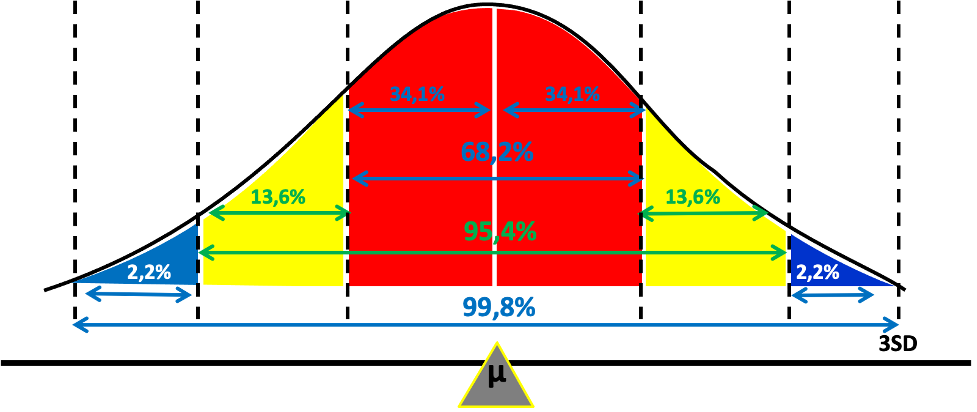
ALLA RICERCA DEL ” µ ” E DELLA SD
Bene, da tutte le disquisizioni sin qui fatte abbiamo tratto un’importante conclusione:
La distribuzione normale può essere utilizzata anche in relazione ai rendimenti di un titolo.
Certo, questo è vero con molti caveat, distinguo, “ma anche no”, etc. etc. Tuttavia, per le nostre finalità, possiamo accettare questa fondamentale affermazione e analizzarne le conseguenze.
Il primo passo è trovare l’equivalente di quello che, nella distribuzione normale, rappresenta il valore centrale, ossia la media (indicata con la lettera greca “µ” nella figura qui sopra.
Per i titoli, possiamo assumere come valore centrale la quotazione attuale.
Ci manca ancora la standard deviation (SD), ossia le misura delle fluttuazioni dei rendimenti e, purtroppo, no SD, no Distribuzione Normale, no party. Come facciamo allora, a procurarcela?
Soluzione 1 – Me la calcolo io
Se proprio sei così diligente e bravo, qui trovi le istruzioni per un calcolo semplice che farebbe storcere il naso a qualcuno, in quanto non usa i rendimenti logaritmici (log-return), ma abbiamo promesso di non avventurarci in matematiche arcane.
Abbiamo anche preparato un foglio Googlesheet che abbiamo già condiviso con i nostri studenti del corso FreeTrade e che magari condivideremo anche con te e gli altri studenti del corso Option Fundamentals, dove comunque usiamo i rendimenti logaritmici, per far contenti gli esperti.
Soluzione 2 – la volatilità storica o quella implicita sono la SD!
La SD su base annuale è la “volatilità storica” (HV) di un titolo che trovate già calcolata dappertutto, basta cercarla.
Anche qui, l’affermazione del titolo (e la successiva) potrebbero essere spiegate sia con riferimento ai calcoli, sia con riferimento all’utilizzo della volatilità nella formula di Black & Scholes. Tuttavia, per semplicità, prendile per buone.
La differenza chiave è che la HV riflette i passati andamenti del titolo; l’altra, la volatilità implicita (IV) riflette invece l’idea del mercato su quella che sarà la volatilità nel futuro. Ma non preoccuparti, avremo modo di approfondire questi concetti nel corso “Options Fundamentals”.
Partendo da queste affermazioni, con una HV – ad esempio – del 20% possiamo ipotizzare che un titolo che vale 50$ tra un anno sarà tra in un range compreso tra 40 e 50$, con una probabilità del 68,2%. Se poi vuoi usare la IV invece, nessun problema, ma presta attenzione al fatto che la HV riflette andamenti passati, ma “certi”.
La IV invece è legata ai movimenti di domanda e offerta e a volte può essere oggetto di distorsioni di breve termine dovuti a temporanei imbalance di domanda e offerta.
Qualsiasi piattaforma di trading, salvo forse qualcuna di quelle italiane (dalle quali, come sai, ci teniamo a debita distanza), ti fornisce la volatilità storica di un titolo. Qui di seguito, trovi un esempio con la piattaforma Tradestation, così non potrai dirci che parliamo sempre di Interactive Brokers o Tastyworks 🙂
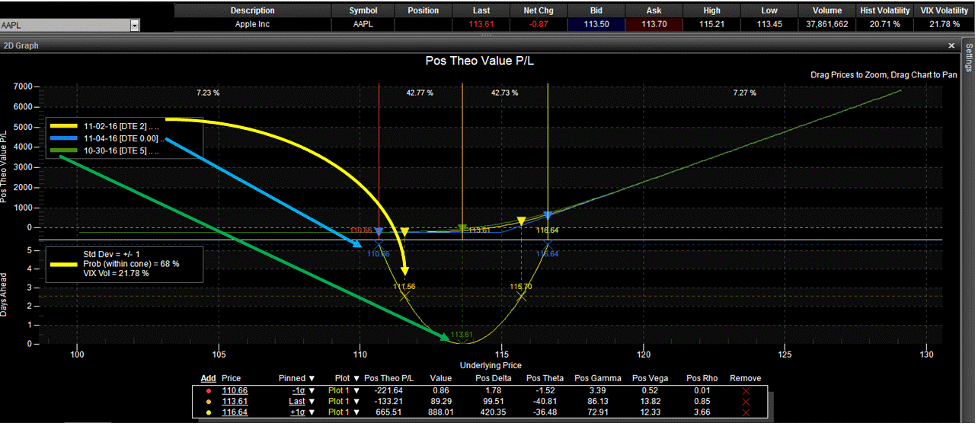
Come vedi, il box in basso ti dà il range atteso di AAPL a ±1 SD (qui indicata con la lettera greca “sigma”) alla data del 4/11 in questo caso. La volatilità usata è indicata nel box al centro-sinistra, mentre la curva gialla in basso in indica il valore del range per scadenze intermedie, come indicato dalle 3 frecce che abbiamo aggiunto noi. Il tutto fa ovviamente riferimento ai valori del sottostante (sempre la nostra cara Apple, ai tempi in cui venne effettuato questo screenshot)
Ovviamente, ogni piattaforma ha le sue specificità. Se invece la tua piattaforma proprio non vuol saperne di calcolare SD e range attesi, oltre a suggerirti di cambiarla, eccoti una formuletta semplice che ti fornisce un’accettabile approssimazione della SD.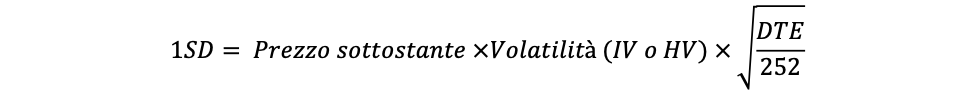
DTE, nella formula, indica il numero di giorni che mancano alla scadenza, ovvero l’orizzonte temporale che ti interessa per le stime, per esempio, con DTE = 10, la formula ti dà il movimento atteso da qui a 10 gg in base ai parametri di volatilità del titolo. Da notare che potrai trovare alcune formule con al denominatore della frazione 252 (i giorni in un anno in cui è aperta la borsa) o 365.
Se prendiamo Apple, con 5 giorni alla scadenza, come nel caso della figura sopra vista il calcolo ci dà un range 116,51 – 110,71 (usando 365 al denominatore) ovvero 117,1 – 110,12 (usando 252). In entrambi i casi, un dato sostanzialmente simile a quello della piattaforma di trading.
Bene, ci siamo quasi.
Alla fine della fiera ‘sto range di prezzi, se fossi tu a dover prezzare un’opzione, che informazioni ti dà?
Beh, un po’ di cose te le racconta, ma di certo quella importante e basilare è che, le call con strike maggiore di 116,51 e le put con strike inferiore a 110, tendono a perdere valore molto più rapidamente delle loro colleghe che rientrano nel range, perché sono vittime della SD e della Distribuzione Normale, che ineluttabilmente concedono loro poche chance di finire ITM.
VABBE’, MA COSA ME NE FACCIO DI TUTTI ‘STI RAGIONAMENTI??
Domanda legittima, se hai avuto la pazienza di leggerci fin qui.
Cosa te ne fai di questa informazione, al di là di capire un po’ meglio le dinamiche di prezzo delle opzioni?
Se sei trader “tradizionale”, ossia uno di quelli che comprano (o sperano di comprare) sui minimi e vendere sui massimi, te ne fai poco o niente.
In sostanza, ti stiamo dicendo che, tra 5 giorni c’è un 68% circa di possibilità che Apple stia più o meno 2,2$ al di sopra o 2,2$ al di sotto del valore attuale. E tu, cosa potresti fare? Vendere? Comprare?
Vedi, cara amica o caro amico, nell’approccio probabilistico che abbiamo sin qui visto c’è tutta la differenza tra chi cerca nell’angolo di Gann o nell’analisi tecnica la chiave per capire se il titolo sale o scende. Perché lui si deve schierare se vuole far soldi, cioè deve dire: “Apple sale” e magari spiegarlo con un oscillatore, un pattern grafico o altre motivazioni “tecniche”, geometriche, planetarie, ovvero, se proprio è un gran figo, con i punti di forza quantici, il bosone di Higgs, gli astri di Branko, insomma, fai tu.
Noi, poveri option traders, non abbiamo necessariamente bisogno di scommettere su Apple in salita o in discesa. Ci basta ragionare su dove è probabile che Apple stia o non stia ad una certa data. Possiamo puntare sul fatto che resti in quel range, cioè tra 116,51 e 110,71$, che lo sfori, possiamo combinare le due ipotesi se ne scegliamo una e ci accorgiamo che è sbagliata. Insomma, siamo come chi ha a disposizione la Sesta Flotta del Mediterraneo e chi invece va alla guerra col gommone.
Questo è il bello delle opzioni e – devi crederci – se questo scritto non ti è risultato del tutto indigesto, sei già un bel passo avanti nel percorso che ti porterà a capirle e a sfruttarle.
Come?
Te lo spiegheremo nelle prossime sessioni del corso Option Fundamentals di www.optiontraders.it.